Beweis: kürze das n in Zähler und Nenner
Ein paar schöne Beweise
Beh.: 1 = 2
Bew.: x² - x² = x² - x²
<=> x (x - x) = (x + x)(x - x) (linke Seite ausgeklammert, rechte Seite binom.
Formel)
<=> x = x + x (gekürzt)
<=> 1 = 2 (durch x)
1
Beh.:
---- = 0 ( oo = unendlich )
oo
1
Beweis: wir beginnen mit --- = oo ,
0
drehen beide Seiten um 90 Grad nach links und
erhalten -10 = 8 ; nun ziehen wir auf jeder Seite 8 ab und erhalten -18 = 0 .
Nun drehen wir beide Seiten wieder um 90 Grad nach rechts und erhalten 1
---- = 0 .
oo
THEOREM : alle natürlichen Zahlen sind
interessant
BEWEIS: Angenommen, es wäre nicht so; dann existiert eine kleinste natürliche
Zahl, die nicht interessant ist.
Diese Zahl ist offensichtlich interessant, was der Annahme, daß sie nicht
interessant ist, widerspricht. Dieses ist ein Widerspruch, also muß die Annahme
falsch sein, womit die Behauptung gezeigt ist.
Beh: Alle Dreiecke sind gleichseitig.
Bew.:
Gegeben sei ein beliebiges Dreieck ABC.
Man errichtet die Mittensenkrechte auf AB in D und schneide sie mit der
Winkelhalbierenden in C um E zu erhalten.
Dann errichte man das Lot von E auf AC in F und von E auf BC in G.
Ausserdem zeichne man noch die Strecken AE und BE.
Skizze (etwas schief wegen ASCII und so):
C *
/|\
/ | \
/ / \
/ | \
/ | \
/ / \
/ | \
/ | \
/ / \
/ | \
/ | \
F*- / \
/ -- | -*G
/ -- | --- \
/ -- E/ ---- \
/ --*---- \
/ --- | - \
/ -- | -- \
/ -- | -- \
/ -- | -- \
/
-- | -- \
/-- | -- \
A*----------------------*-------------------*B
D
1. Die Winkel ECF und ECG sind gleich. Die Winkel EFC und EGC sind beide rechte Winkel. Da die Dreiecke ECF und ECG ausserdem EC gemeinsam haben, muessen sie kongruent sein (SWW). Also gilt CF=CG und EF=EG.
2. Die Strecken DA und DB sind gleich. Die Winkel EDA und EDB sind beide rechte Winkel. Da die Dreiecke EDA und EDB ausserdem ED gemeinsam haben, muessen sie kongruent sein (SWS). Also gilt EA=EB.
3. Die Winkel EGB und EFA sind beide rechte Winkel. Ausserdem gilt EF=EG (1.) und EA=EB (2.). Deshalb sind auch die beiden Dreiecke EGB und EFA kongruent (SSW). Also gilt FA=GB.
4. Da CF=CG (1.) und FA=GB (3.) muss nach
Addition der Strecken auch CA=CB gelten.
Damit ist bewiesen, dass zwei beliebige Seiten in einem Dreieck gleich lang
sind. Also muss dies auch fuer alle 3 Seiten gelten.
(QED)
Lemma1: All horses are the same
color.
Proof (by induction):
Case n=1: In a set with only one horse, it is obvious that all horses in
that set are the same color.
Case n=k: Suppose you have a
set of k+1 horses. Pull one of these horses out of the set, so that you have k
horses.
Suppose that all of these horses are the same color. Now put back the horse
that you took out, and pull out a different
one. Suppose that all of the k horses now in the set are the same color.
Then the set of k+1 horses are all the same
color. We have k true => k+1 true; therefore all horses are the same color.
Theorem1: All horses have an infinite number of legs.
Proof (by intimidation):
Everyone would agree that all horses have an even number of legs. It is
also well-known that horses have forelegs in
front and two legs in back. 4 + 2 = 6 legs, which is certainly an odd
number of legs for a horse to have! Now the only
number that is both even and odd is infinity; therefore all horses have an
infinite number of legs.
However, suppose that there is a horse somewhere that does not have an
infinite number of legs. Well, that would be a
horse of a different color; and by the Lemma, it doesn't exist.
Corollary 1. Everything is the same colour.
Proof. The proof of lemma 1 does
not depend at all on the nature of the object under consideration. The
predicate of the antecedent of the universally-quantified conditional 'For all
x, if x is a horse, then x is the same colour,' namely 'is a horse' may be
generalized to 'is anything' without affecting the validity of the proof; hence,
'for all x, if x is anything, x is the same colour.'
Corollary 2. Everything is white.
Proof. If a sentential formula in
x is logically true, then any particular substitution instance of it is a true
sentence. In particular
then: 'for all x, if x is an elephant, then x is the same colour' is true. Now
it is manifestly axiomatic that white elephants exist (for
proof by blatant assertion consult Mark Twain 'The Stolen White Elephant').
Therefore all elephants are white. By corollary 1 everything is white.
Theorem 2. Alexander the Great did not exist and he had an infinite number of limbs.
Proof. We prove this theorem in
two parts. First we note the obvious fact that historians always tell the truth
(for historians always take a stand, and therefore they cannot lie). Hence we
have the historically true sentence, 'If Alexander the Great existed, then he
rode a black horse Bucephalus.' But we know by corollary 2 everything is white;
hence Alexander could not have ridden a black horse. Since the consequent of
the conditional is false, in order for the whole statement to be true the
antecedent must be false. Hence Alexander the Great did not exist.
We have also the historically true statement that Alexander was warned by an
oracle that he would meet death if he crossed a certain river. He had two legs;
and 'forewarned is four-armed.' This gives him six limbs, an even number, which
is certainly an odd number of limbs for a man. Now the only number which is even
and odd is infinity; hence Alexander had an infinite number of limbs. We have
thus proved that Alexander the Great did not exist and that he had an infinite
number of limbs.
Satz: Alle natuerlichen Zahlen sind gleich
Beweis: Wir zeigen: falls für eine natuerliche Zahl m gilt max(a,b) = m, dann
folgt a = b (a , b nat. Zahlen).
(daraus folgt offenbar die Behauptung)
Induktion über m:
Induktionsanfang (m = 1) : max(a,b) = 1 => a = b = 1 o.k.
Induktionsschritt (m -> m + 1 ): Fuer m sei die Behauptung bewiesen.
max(a,b) = m + 1 => max(a -
1 , b - 1) = m
=> a - 1 = b - 1 (nach Induktionsannahme)
=> a = b
QED
Satz: Mathematiker sind konvergent.
Beweis: Mathematiker sind monoton und beschränkt. q.e.d.
Behauptung: Eine Katze hat neun Schwänze.
Beweis: Keine Katze hat acht Schwänze. Eine Katze hat einen Schwanz mehr als
keine Katze.
Deshalb hat eine Katze neun Schwänze, qed.
![]()
Beweis: kürze das n in Zähler und Nenner
Beh.: -1 = 1
Bew.:
i = sqrt(-1)
<=> i * i = sqrt(-1) * sqrt(-1) = sqrt ((-1)*(-1))
<=> i^2 = sqrt(1)
<=> -1 = 1
Beh.: 4 = 5
Bew.: Sei b beliebig, a = b+1 |multipliziere beide Seiten mit (a-b)
<=> a² - ab = ab + a - b² - b
<=> a² + b² = 2 ab + a - b
Setze a = 4, b = 4.
Wir erhalten 16 + 16 = 32 + 4 - 4, also eine wahre Identität.
Darum ist auch a = b + 1 richtig, und wegen a = b = 4 gilt 4 = 5.
Beh.: 5 = 7
Bew.: Sei b = 1, a = 1,5.
Dann: 10a = 15 b und 14 a = 21 b
Beide Gleichungen subtrahieren: 14 a - 10 a = 21 b - 15 b
<=> 15 b - 10 a = 21 b - 14 a
<=> 5 (3b-2a) = 7 (3b-2a)
<=> 5 = 7
a = b + c
<=> a (a - b) = (b + c) (a - b)
<=> a² - ab = ab - b² + ac - bc | -ac
<=> a² - ab - ac = ab - b² - bc
<=> a (a - b - c) = b (a - b - c)
<=> a = b
Beh.: 4 = 5
Bew.: 16 - 36 = 25 - 45
<=> 16 - 36 + 4,5² = 25 - 45 + 4,5²
<=> 4² - 2*4,5*4 + 4,5² = 5² - 2*4,5*5 + 4,5²
<=> (4 - 4,5)² = (5 - 4,5)²
<=> 4 - 4,5 = 5 - 4,5
<=> 4 = 5
Beh.: 4 = 5
Bew.: Sei a = b + c.
Dann 5a=5b + 5c und 4b + 4c = 4a
Beide Gleichungen addieren:
4b+4c+5a = 5b+5c+4a
<=> 4b+4c-4a = 5b+5c-5a
<=> 4 (b + c - a) = 5 (b + c - a)
<=> 4 = 5
Beh.: 4 = 5
Bew.: Sei a=4, b=5, c=(a+b)/2.
Dann a+b=2c, also a=2c-b und 2c-a=b
Beide Gleichungen multiplizieren:
a (2c-a) = b (2c-b)
<=> a² - 2ac = b² - 2bc
<=> a² - 2ac + c² = b² - 2bc + c²
<=> (a-c)² = (b-c)²
<=> a-c = b-c
<=> a=b, d.h. 4=5
5 + 2 = 7
<=> 5 * (5 + 2) = 5 * 7
<=> 25 + 10 = 35
<=> 25 + 10 - 35 = 35 - 35
<=> 25 + 10 - 35 = 35 - 35 - 14 + 14
<=> 25 + 10 - 35 = 35 + 14 - 49
<=> 5 * (5 + 2 - 7) = 7 * (5 + 2 - 7)
<=> 5 = 7
q.e.d
Beh.: 3 = 4
Bew.: Setze x=3 und y=4
Dann: x+y = 7 |*(x-y)
<=> (x+y)*(x-y) = 7*(x-y)
<=> x²+xy-xy-y² = 7x-7y |+y²-7x
<=> x²-y²+y²-7x = 7x-7y+y²-7x
<=> x²-7x = y²-7y |+49/4
<=> x²-7x+49/4 = y²-7y +49/4
<=> (x-7/2)² = (y-7/2)² |Wurzel ziehen
<=> x-7/2 = y-7/2 |+7/2
<=> x = y
<=> 3 = 4
q.e.d.
Beh.: 4 = 5
Bew.: 1 = 1
4 5
<=> --- = ---
4 5
1 1
<=> 4 * --- = 5 * ---
1 1
<=> 4 = 5
q.e.d.
(i ist hier natürlich die imaginäre Einheit, also i²= -1)
(i
x) (i 2 pi x /(2 pi))
e = e
(x /(2 pi))
(2 pi i)
= e
(x /(2 pi))
= 1
= 1
---> exp(i x) = 1 , für alle x !
Theorem : Alle Zahlen sind = 0.
Beweis: Sei a=b. Dann
a = b
<=> a² = ab
<=> a² - b² = ab - b²
<=> (a + b)(a - b) = b(a - b)
<=> a + b = b
<=> a = 0, qed
Theorem: 1 DM = 1 Pfennig.
Beweis: 1 DM = 100 Pf
= (10 Pf)²
= (0,1 DM)²
= 0,01 DM
= 1Pf, qed.
Object: to prove that i < 0 ( that is, sqrt(-1) < 0 )
Well, ( 0.5 + sqrt(3/4)*i )^3 =
(-1)^3 (It's true. It's the next statement that is false.)
which means that ..5 + sqrt(3/4)*i = -1
So then 1 + sqrt(3)*i = -2
<=> sqrt(3)*i = -1
<=> i = -1/sqrt(3)
Therefore i is a negative number. QED.
Theorem: n=n+1
Beweis: (n+1)² = n² + 2n + 1 | -(2n+1)
<=> (n+1)² - (2n+1) = n² | -n(2n+1)
<=> (n+1)² - (n+1)(2n+1) = n² - n(2n+1) | +1/4(2n+1)²
<=> (n+1)² - (n+1)(2n+1) + 1/4(2n+1)² = n² - n(2n+1) + 1/4(2n+1)²
<=> [ (n+1) - 1/2(2n+1) ]² = [ n - 1/2(2n+1) ]²
<=> (n+1) - 1/2(2n+1) = n - 1/2(2n+1)
<=> n+1 = n qed.
Theorem: log(-1) = 0
Beweis: a) log[(-1)²] = 2 log(-1)
Andererseits: b) log[(-1)²] = log(1) = 0
Aus a) und b) folgt: 2* log(-1) = 0 und damit log(-1)=0
Beh.: ln(2) = 0
Beweis:
Bekanntlich ist ln 2 = 1 - 1/2 + 1/3 - 1/4 + 1/5 - 1/6 ...
Umordnen liefert:
ln 2 = (1 + 1/3 + 1/5 + 1/7 ...) - (1/2 + 1/4 + 1/6 + 1/8 ...)
Somit:
ln 2 = (1 + 1/3 + 1/5 + 1/7 ...) + (1/2 + 1/4 + 1/6 + 1/8 ...) - 2 * (1/2 + 1/4
+ 1/6 + 1/8 ...)
Aus dieser und der oberen Reihe folgt:
ln 2 = (1 + 1/2 + 1/3 + 1/4 + 1/5 ...) - (1 + 1/2 + 1/3 + 1/4 + 1/5 ...)
und somit:
ln 2 = 0, qed.
Sei x das Gewicht des Elefanten und y das Gewicht der Muecke. Sei d der
Unterschied.
x = y + d |*(x-y)
x^2 - xy = xy + xd - y^2 - yd |-xd
x^2 - xy -xd = xy - y^2 - yd
x(x - y - d) = y(x - y - d) | : (x - y - d)
x=y
d.h. Das Gewicht des Elefanten ist gleich dem Gewicht einer Muecke !!!
Beh.: -a = a
Bew.: n sei gerade.
-a=(-a)^1
=(-a)^n/n
=[(-a)^n]^1/n (Eine negative
Zahl hoch einer geraden Zahl ergibt ihren Betrag.)
= [a^n]^1/n
= a^n/n
= a^1
= a
Beh.: Unendlich = 2
Beweis:
Wieviele Symmetrieachsen hat ein Kreis? Antwort: Unendlich viele!
Jetzt teilen wir alles durch zwei! Wieviele Symmetrieachsen hat der Halbkreis?
Antwort: Eine einzige!
Daraus folgt: Unendlich=2. q.e.d.
Behauptung: Ein Krokodil ist länger als breit
Beweis:
Lemma 1: Ein Krokodil ist länger als es grün ist
Man betrachte ein Krokodil. Es ist oben lang und unten lang, aber nur oben grün.
Also ist ein Krokodil länger als es grün ist.
Lemma 2: Ein Krokodil ist grüner als breit
Man betrachte wieder ein Krokodil. Es ist grün entlang Länge und Breite, aber
nur breit entlang der Breite.
Also ist ein Krokodil grüner als breit.
Aus Lemma 1 und 2 folgt: Das Krokodil ist länger als breit.
Theorem: ln(2) = 0
Proof:
Consider the series equivalent of ln 2: ln 2 = 1 - 1/2 + 1/3 - 1/4 + 1/5 - 1/6
...
Rearange the terms: ln 2 = (1 + 1/3 + 1/5 + 1/7 ...) - (1/2 + 1/4 + 1/6 + 1/8
...)
Thus: ln 2 = (1 + 1/3 + 1/5 + 1/7 ...) + (1/2 + 1/4 + 1/6 + 1/8 ...) - 2 *
(1/2 + 1/4 + 1/6 + 1/8 ...)
Combine the first to series: ln 2 = (1 + 1/2 + 1/3 + 1/4 + 1/5 ...) - (1 + 1/2
+ 1/3 + 1/4 + 1/5 ...)
Therefore: ln 2 = 0 q.e.d
Beh.: 2x = x
Bew.: x² = x*x = x+x+x+...+x (* x-mal aufsummiert *)
Differenzieren nach x ergibt:
2x = (1+1+1+...+1) (* x-mal aufsummiert *)
<=> 2x = x q.e.d.
Beh.: 3 = 5
Bew.: 25 - 15 - 10 = 15 - 9 - 6
<=> 5 (5 - 3 - 2) = 3 (5 - 3 - 2)
<=> 5 = 3 q.e.d.
Beh.: 4 > 12
Bew.: Zu beiden Seiten der offensichtlichen Ungleichung 7 > 5 addieren wir -8
und erhalten 7 - 8 > 5 - 8 oder -1 > -3. Jetzt multiplizieren wir auf beiden
Seiten der erhaltenen Ungleichung mit -4 und erhalten (-1)*(-4) > (-3)*(-4) bzw.
4 > 12 q.e.d.
Beh.: 1/4 > 1/2
Bew.: sin (pi/6) = sin (pi/6)
<=> log sin (pi/6) = log sin (pi/6)
<=> 2 log sin (pi/6) > log sin (pi/6)
<=> log sin² (pi/6) > log sin (pi/6)
<=> sin² (pi/6) > sin (pi/6)
<=> (1/2)² > 1/2
<=> 1/4 > 1/2 q.e.d.
Beh.: oo = -1
Bew.: Sei x = 1 + 2 + 4 + 8 + 16 + ...
Daraus folgt 2x = 2 + 4 + 8 + 16 + 32 + ...
Also gilt 2 x + 1 = x
<=> x = -1
Das heißt 1 + 2 + 4 + 8 + 16 + ... = -1
und damit 00 = -1
Beh.: 00 < -1
Bew.: Es ist offensichtlich, daß 1/(n+1) < 1/n.
Darum folgt ...1/3 < 1/2 < 1/1 < 1/0 < 1/-1 < 1/-2 < 1/-3 < ...
Das bedeutet, daß 1/0 < 1/-1 oder oo < -1
Beh.: 1 <> 1 (<> steht hier für ungleich)
Bew.: Aus der Bruchrechnung ist bekannt, daß aus der Gleichung zweier
gebrochener Zahlen a/b = c/d
die Gleichung (a-b)/(b-d) = a/b folgt,
da in beiden Fällen die Grundbedingung für die Gleichheit zweier Brüche ad=bc
gilt.
Es seien nun x,y,z solche Zahlen, daß folgende Gleichung gilt:
(3y-4z)/(3y-8z) = (3x-z)/(3x-5z)
Wir wenden die erwähnte Regel an und erhalten
(3y-4z-(3x-z))/(3y-8z-(3x-5z)) = (3y-4z)/(3y-8z) oder nach Auflösen der Klammern
(3y-3z-3x)/(3y-3z-3x) = (3y-4z)/(3y-8z)
Auf der linken Seite dieser Gleichung steht ein Bruch, dessen Zähler und Nenner
gleich sind, die linke Seite ist also =1. Zähler und Nenner des Bruches auf der
rechten Seite sind ungleich, also ist die rechte Seite ungleich 1. Also ist 1
ungleich 1, q.e.d.
Beh.: Das Quadrat einer beliebigen Zahl ist gleich 1
Bew.: Es sei x=y=m²/4 (m natürliche Zahl) (1)
Daraus folgt sqrt(x) = sqrt(y) (2)
Wir subtrahieren von der Gleichung (1) die Gleichung (2) und erhalten folgende
Kette von Gleichungen:
x-sqrt(x) = y-sqrt(y)
<=> x-y = sqrt(x) - sqrt(y)
<=> (sqrt(x)+sqrt(y))*(sqrt(x)-sqrt(y)) = sqrt(x) - sqrt(y)
<=> sqrt(x) + sqrt(y) = 1
<=> 2 sqrt(x) = 1
In die letzte Gleichung setzen wir Gleichung (1) ein:
2 sqrt(m²/4) = 1, also m²=1
q.e.d.
Beh.: Alle Katzen haben die gleiche Augenfarbe
Bew.: Für n=1 ist die Behauptung offensichtlich. Wir nehmen jetzt an, daß je n
Katzen die gleiche Augenfarbe haben, und beweisen, daß das auch für je n+1
Katzen gilt.
Wir nehmen n+1 willkürlich ausgewählte Katzen und numerieren sie. Nach der
Induktionsvorraussetzung haben die Katzen mit den Nummern 1 bis n die gleiche
Augenfarbe und auch die n Katzen mit den Nummern 2 bis n+1. Zu beiden Mengen
gehört z.B. die Katze Nr. 2, also haben alle n+1 Katzen die gleiche Augenfarbe.
q.e.d.
Ist der Papst ein Ausserirdischer?
Wenn ein Individiuum ein Mensch ist, dann ist es wahrscheinlich nicht der Papst
(1 : 6*10^9)
Johannes Paul II ist der Papst
=> Johannes Paul II ist ziemlich sicher kein Mensch
(aus "Der Hund, der Eier legt" von Hans-Peter Beck-Bornholt und Hans-Hermann
Dubben)
Vielen Dank an Karl Kechele, der mir diese Beweise und einige Mathewitze
geschickt hat!
Ist Johannes Paul II der Papst?
Wenn ein Individiuum ein Mensch ist, dann ist es wahrscheinlich nicht der Papst
(1 : 6*10^9)
Johannes Paul II ist ein Mensch
=> Johannes Paul II ist so gut wie sicher nicht der Papst
(aus "Der Hund, der Eier legt" von Hans-Peter Beck-Bornholt und Hans-Hermann
Dubben)
Nur wer nicht Lotto spielt, kann sicher gewinnen!
Wenn Sie Lotto spielen, gewinnen Sie wahrscheinlich nichts (1 : 14*10^6)
Sie haben im Lotto gewonnen
=> Also haben sie höchstwahrscheinlich nicht Lotto gespielt
(aus "Der Hund, der Eier legt" von Hans-Peter Beck-Bornholt und Hans-Hermann
Dubben)
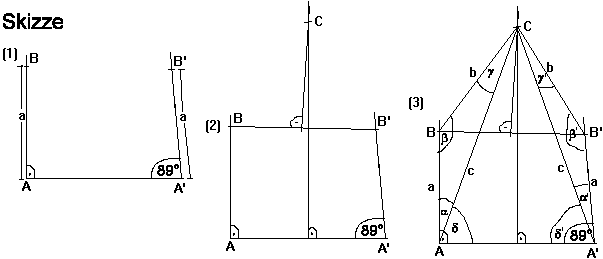
Beh.: 90 Grad = 89 Grad
Beweis:
(1)
Zeichnen einer Strecke A A'
Einzeichnen zweier Halbgeraden zu A und A'
Kreis um A (A') mit Radius a -> B (B')
(2)
Verbindungsstrecke B B' einzeichnen
Mittelsenkrechte zu AA' und BB' einzeichnen
Schnittpunkt der beiden Mittelsenkrechten ergibt Punkt C
(3)
Einzeichnen der Strecken CB, CA, CB', CA'
C liegt auf der Mittelsenkrechten zu AA' -> [CA] = [CA'] -> c
C liegt auf der MS zu BB' -> [BC] = [B'C] -> b
a nach Konstruktionsvoraussetzung gleich lang.
=> Dreieck ABC hat gleichlange Seiten wie Dreieck A'B'C.
=> Dreieck ABC kongruent Dreieck A'B'C
2 kongruente Dreiecke haben gleiche Innenwinkel
=> alpha=alpha' ; beta=beta' ; gamma=gamma'
Im Dreieck AA'C gilt:
delta=delta' (Basiswinkel im gleichschenkligen Dreieck)
=>
alpha + delta = 90 Grad
alpha' + delta' = 89 Grad
Es gilt: alpha=alpha' ; delta=delta'
=> alpha + delta = 90 Grad = 89 Grad = alpha' + delta'
q.e.d.
Skizze hierzu: