In der Praxis werden hauptsächlich Asynchronmotoren wegen ihres wartungsarmen und robusten Betriebsverhaltens als drehzahlgesteuerte oder drehzahlgeregelte Antriebe eingesetzt. Die Drehfrequenz n wird über die Frequenz f der Betriebsspannung gesteuert. Sie ist proportional zur Frequenz
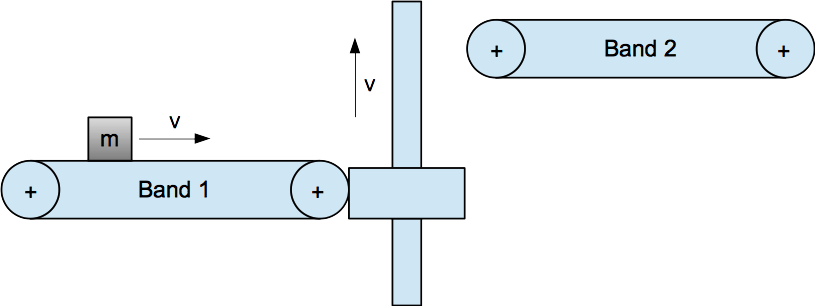
Ein Förderband 1 soll Werkstücke der Masse m mit der Geschwindigkeit v transportieren. Anschließend soll der Hubantrieb die Wekstücke zum Förderband 2 heben. Das Förderband 2 transportiert die Werkstücke nach rechts. Für diese Antriebsaufgabe müssen drei passende Asynchronmotore und Frequenzumrichter ausgewählt werden. Die komplette Installation und Inbetriebnahme ist zu planen.
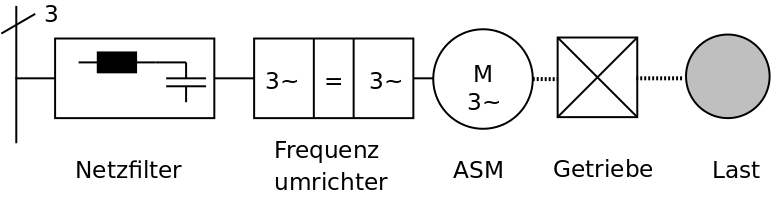
Jeder Antrieb besteht aus einer mechanischen Last (Arbeitsmaschine) und einem Motor. Der Motor muss der Arbeitsmaschine angepasst werden. Die Drehfrequenz des Motors wird mit einem Frequenzumrichter gesteuert. Das Getriebe wandelt das Drehmoment und die Drehfrequenz.
Der Gesamtwirkungsgrad berechnet sich aus dem Produkt aller Teilwirkungsgrade:
ηges = ηFU⋅ηMotor⋅ηGetriebe
Der Verlauf des Drehmoments und der mechanischen Leistung ist abhängig vom Typ der Arbeitsmaschine.
| Arbeitsmaschine | Hebezeuge | Kalander | Pumpen Lüfter Zentrifugen Rührwerke |
Wickler Plandrehmaschinen Rundschälmaschinen |
|---|---|---|---|---|
| Drehmoment | M = konstant | M ~ n | M ~ n2 | M ~ 1/n |
| Leistung | P ~ n | P ~ n2 | P ~ n3 | P = konstant |
| Größe | Formel | Erläuterung |
|---|---|---|
| Winkelgeschwindigkeit | ω=2π/T ω=2π⋅n |
Die Winkelgeschwindigkeit ist der Quotient aus dem Vollwinkel (360°) und der Zeit T für eine Umdrehung der Welle. |
| Winkelbeschleunigung | α=Δω/Δt | Je schneller sich der Winkel ändert, desto größer ist die Winkelbeschleunigung. |
| Drehmoment | M = F⋅r | Das Drehmoment ist das Produkt aus Kraft F mal Hebelarm r. |
| mechanische Leistung | P = M⋅ω | Die mechanische Leistung ist proportional zum Drehmoment M und proportional zur Winkelgeschwindigkeit ω. |
| Trägheitsmoment | J=0,5⋅m⋅r2 | Das Trägheitsmoment ist proportional zur Masse m des Zylinders und proportional zum Quadrat des Zylinderradius r. |
| Beschleunigungsmoment | MB = J⋅α | Das Beschleunigungsmoment ist proportional zum Trägheitsmoment und proportional zur Winkelbeschleunigung. |
Für jeden Antrieb muss das Drehmoment
M = F⋅r (1)
aufgebracht werden.
Die mechanische Leistung P eines rotierenden Zylinders ist das
Produkt aus Umfangsgeschwindigkeit v und der Kraft, die am Umfang des
Zylinders wirkt:
P = F⋅v (2)
Setzt man die Umfangsgeschwindigkeit v = 2⋅π⋅r/T in Gleichung (2) ein, erhält man:
P = F⋅2⋅π⋅r/T (T ist die Zeit für eine Umdrehung des Zylinders, 1/T ist die Drehfrequenz n)
Mit Gleichung (1) erhält man dann:
P = M⋅2⋅π⋅n
Die mechanische Leistung P, die der Motor aufbringen muss, ist also
proportional zum Drehmoment M und proportional zur Drehfrequenz n des
Motors.
Die Bemessungsdrehfrequenz der Arbeitsmaschine kann wegen der Massenträgheit nur mit einer gewissen Verzögerung erreicht werden. Um die Massenträgheit zu überwinden, muss
der Motor während des Hochlaufvorgangs zusätzlich zum Lastmoment noch
ein Beschleunigungsmoment MB aufbringen. Dieses Beschleunigungsmoment ist proportional zur Masse m, zum Quadrat des Radius r der Antriebsrollen des Förderbandes und umgekehrt proportional zur Änderung der Hochlaufzeit Δt. Das Beschleunigungsmoment eines massiven Zylinders kann wie folgt berechnet
werden:
MB = 0,5⋅m⋅r2⋅2πΔn/Δt
Den Ausdruck:
J = 0,5⋅m⋅r2
nennt man Trägheitsmoment. Das Trägheitsmoment J eines rotierenden
Körper bestimmt sein Trägheitsverhalten. Ein hohes Trägheitsmoment der
Arbeitsmaschine verlangt vom Motor ein hohes Beschleunigungsmoment.
Mit ω = 2π⋅n kann für das Beschleunigungsmoment abgekürzt geschrieben werden:
MB = J⋅Δω/Δt