Kondensator
Neben dem Widerstand und der Spule gibt es noch den Kondensator als passives Bauelemente.
Kapazität eines Kondensator
Der Kondensator speichert elektrische Energie. Die
wichtigste Kenngröße des Kondensators ist die Kapazität. Die Kapazität ist ein Maß
für die Speicherfähigkeit von elektrischer Energie.
Definition der Kapazität
Die Kapazität C eines Kondensators wird als Verhältnis der
gespeicherter Ladung Q zu der ladungserzeugenden Spannung U definiert:
Kapazität= Ladungsmenge / Spannung
C= Q/U
Kapazität eines Plattenkondensators
C = ε0 εr A/d
ε0: elektrische Feldkonstante 8,854⋅10-12 As/Vm.
εr : relative Permittivität (Materialkonstante)
A: Plattenfläche
d: Plattenabstand
| Material |
relative Permittivität εr |
| Vakuum |
1 |
| Papier |
1,2 bis 3 |
| Glas |
5 bis 16 |
| Porzellan |
5 bis 6,5 |
| Wasser |
70 bis 88 |
| keramische Werkstoffe |
10 bis 50000 |
Berechnung der Kapazität eines Plattenkondensators
Gespeicherte elektrische Energie
W =0,5 C U2
Berechnung der gespeicherten Energie
Aufgaben
- Nennen Sie drei Anwendungsbeispiele für Kondensatoren.
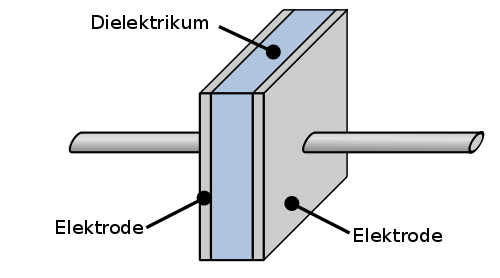
- Beschreiben Sie den Aufbau eines Platten-Kondensators.
- Was versteht man unter Kapazität?
- Wie wird die Kapazität definiert?
- Auf den Platten eines an eine Spannungsquelle von 120 V
angeschlossenen Plattenkondensators befindet sich eine Ladung von 2,4
mAs. Berechnen Sie die Kapazität.
- Wie ändert sich die Kapazität eines Plattenkondensators, wenn man
a) die Plattenfläche vergrößert, b) den Plattenabstand verkleinert.
- Beschreiben Sie die Berechnungsvorschrift (Formel) für die
Berechnung der Kapazität eines Plattenkondensators.
- Was versteht man unter Dielektrikum? Welchen Einfluss hat das
Dielektrikum auf die Kapazität eines Kondensators?
- Berechnen Sie die Kapazität eines Plattenkondensators mit
rechteckförmigen Platten. Die Seite a hat eine Länge von 20 cm, die
Seite b ist 30 cm lang. Zwischen den Platten befindet sich Luft. Die
Platten haben einen Abstand von 1 mm.
- Wie groß ist die Fläche eines Plattenkondensators für C = 1 F? (εr = 1)
- Wie viel elektrische Energie speichert ein 2,2 μF Kondensator,
wenn er an 230 V angeschlossen wird
Zusammnenhang zwischen Spannung und Stromstärke
Nur wenn sich die Spannung u = f(t) an einem Kondensator ändert,
fließt ein
Strom i = f(t):
i = C Δu/Δt
Berechnung des Stromes i = f(t)
Ein- und Ausschalten einer RC-Reihenschaltung
Bedingt durch die Speichereigenschaft von Kondensatoren erreicht
die Kondensatorspannung erst nach einer gewissen Verzögerung ihren
maximalen Wert.
Mit Hilfe des Simulationsprogramms kann untersucht werden, welchen Einfluss
die Energiespeicher auf die Kurvenverläufe von Spannung u(t) und
Stromstärke i(t) haben.
Die Zeitkonstante τ ist das Produkt aus Kapazität und Widerstand.
Aufladevorgang: u(t) = U0(1 - e-t/τ)
i(t) = I0 e-t/τ
Entladevorgang: u(t) = U0 e-t/τ
i(t) = -I0 e-t/τ
Zeitkonstante τ = R⋅C
Nach 5τ ist der Kondensator aufgeladen bzw. entladen.
Aufgaben
- An einem Kondensator liegt eine trapezförmige Spannung.
Simulieren Sie Spannungs- und Stromverlauf.
- Simulieren und beschreiben Sie den Strom- und Spannungsverlauf
für den Ein-und Ausschaltvorgang eine RC-Gliedes. Welchen Einfluss
haben der Widerstandswert und die Kapazität des Kondensators auf den
Strom- und Spannungsverlauf? Wie wird die Zeitkonstante berechnet? Wie
lange dauert es, bis der Kondensator geladen bzw. entladen ist?
- Wie wird die Zeitkonstante τ aus dem Funktionsverlauf u(t)
ermittelt?
- Ein ferngesteuertes Modellauto mit einer Leistung von 40 mW wird
mit einem Kondensator (C = 1 F) als Energiespeicher betrieben. Der
Kondensator wird an einer Spannungsquelle mit 4,5 V aufgeladen. Wie
lange fährt das Modellauto?
- Ein 220 μF Kondensator wurde mit 230 V aufgeladen. Wie groß ist
die Spannung nach 5 Sekunden, wenn er mit einem Widerstand von 1000 Ω
entladen wird?

