Das ohmsche Gesetz
Das ohmsche Gesetz beschreibt den Zusammenhang zwischen Spannung U und Stromstärke I.
Der einfache Stromkeis

Änderung der Quellenspannung I = f(Uq)
Je größer die Quellenspannung Uq, desto größer die Stromstärke I.
Die Quellenspannung ist die Ursache. Der Stromfluss ist die Wirkung.
Formel: I = Uq/R
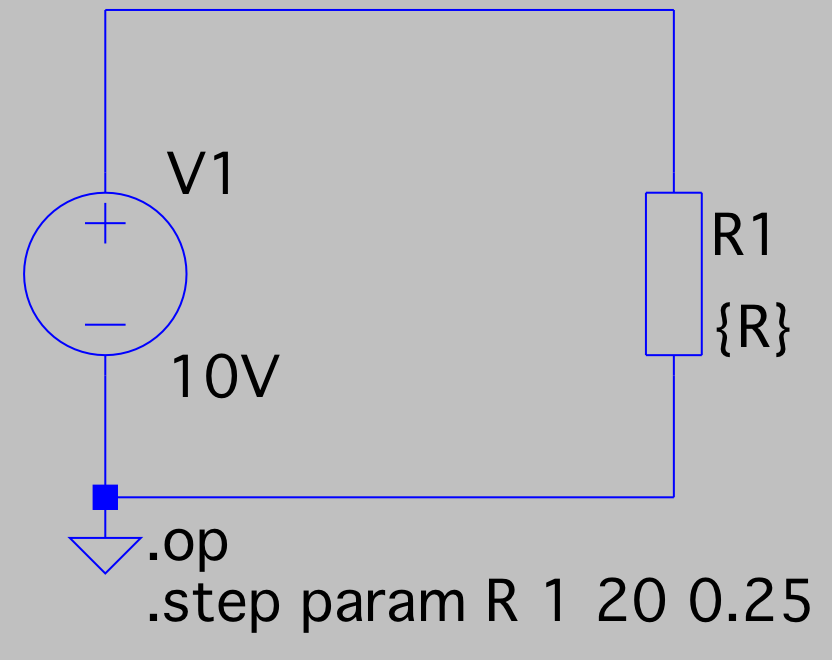
Änderung des Widerstandes I = f (R)
Die Spannung Uq = 10 V bleibt konstand, der Widerstand R wird geändert.
Formel: I = 10 V/R
Mit zunehemenden Widerstand R verringert sich die Stromstärke I.
Änderung der Stromstärke UR = f(I)
Der Widerstand wird an eine Stromquelle angeschlossen. Die Stromstärke wird von 0 bis 10 A geändert.
Am Widerstand R fällt eine Spannung UR ab.
Formel: UR = R⋅I
Die Stromstärke I ist die Ursache. Der Spannungsfall UR ist die Wirkung.
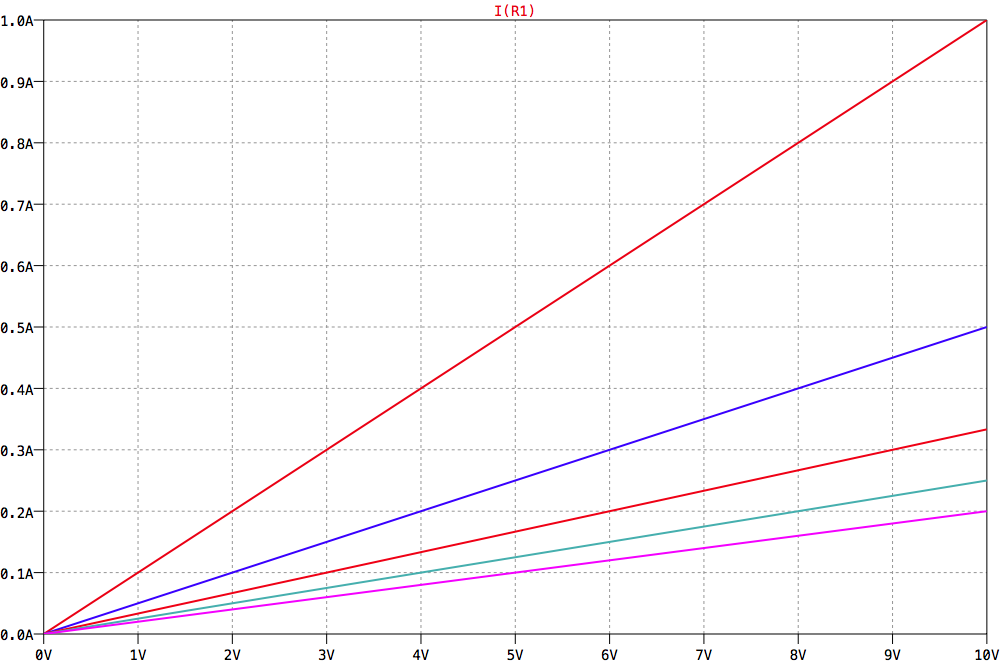
Widerstandskennlinien
Aus den Widerstandkennlinien kann der Widerstand R und der Leitwert G abgelesen werden.
Zusammfassung
| Größe |
Formel |
Beschreibung |
| Spannungsfall |
UR = R⋅I |
Der Spannungungsfall am Widerstand ist proportional zum Produkt aus
Widerstand und Stromstärke. |
| Stromstärke |
I = Uq/R |
Die Stromstärke ist proportional zur Spannung und
umgekehrt proportional zum Widerstand. |
| Widerstand |
R = U/I |
Das Verhältnis von Spannung zur Stromstärke ist konstant.
|
Aufgaben
- Beschreiben Sie den Zusammenhang zwischen Spannung und Stromstärke.
- Wie wird der elektrische Widerstand definiert?
- Wie ändert sich die Stromstärke, wenn bei konstanter Spannung der
Widerstand verringert wird?
- Entwerfen Sie eine Messschaltung für die Ermittlung des ohmschen
Gesetzes.
- Beschreiben Sie die drei Aussagen des ohmschen Gesetzes.
- Simulieren Sie den Zusammenhang I=f(U).
- Simulieren Sie den Zusammenhang I=f(R).
- Durch einen 12 Ω - Widerstand fließt eine Strom von 1,5 A.
Berechnen Sie den Spannungsfall.
- Ein Widerstand von 23 Ω wird an eine Spannung von 230 V
angeschlossen. Berechnen Sie die Stromstärke.
- Ein Widerstand wird an eine Spannung von 230 V angeschlossen. Durch den
Widerstand fließt ein Strom von 1,15 A. Berechnen Sie den Wert des
Widerstandes.

