Der Wechselstromkreis

Im Wechselstromkreis kommen neben dem ohmschen Widerstand auch noch Kapazitäten und Induktivitäten als Verbraucher vor.


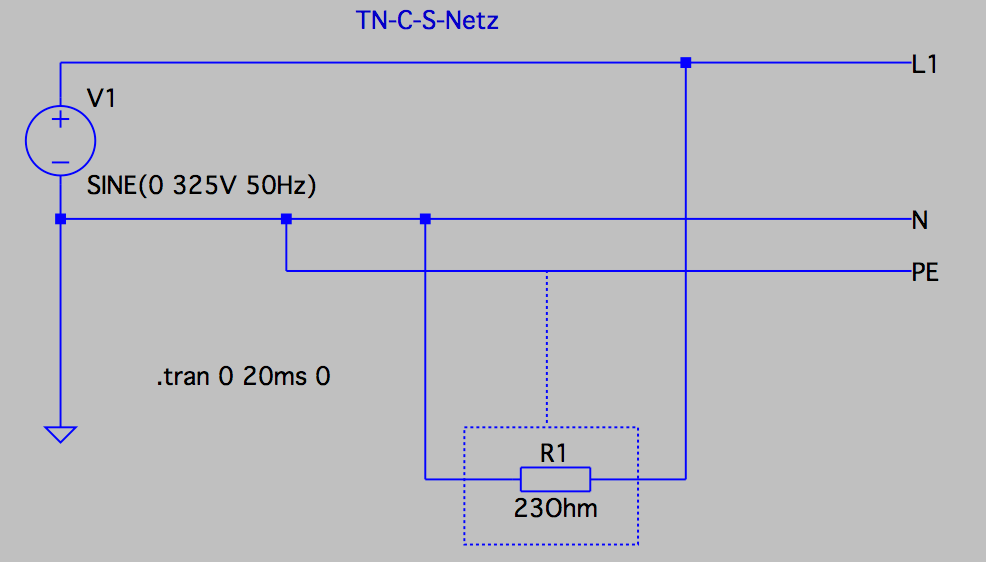
Spannungs- und Stromverlauf


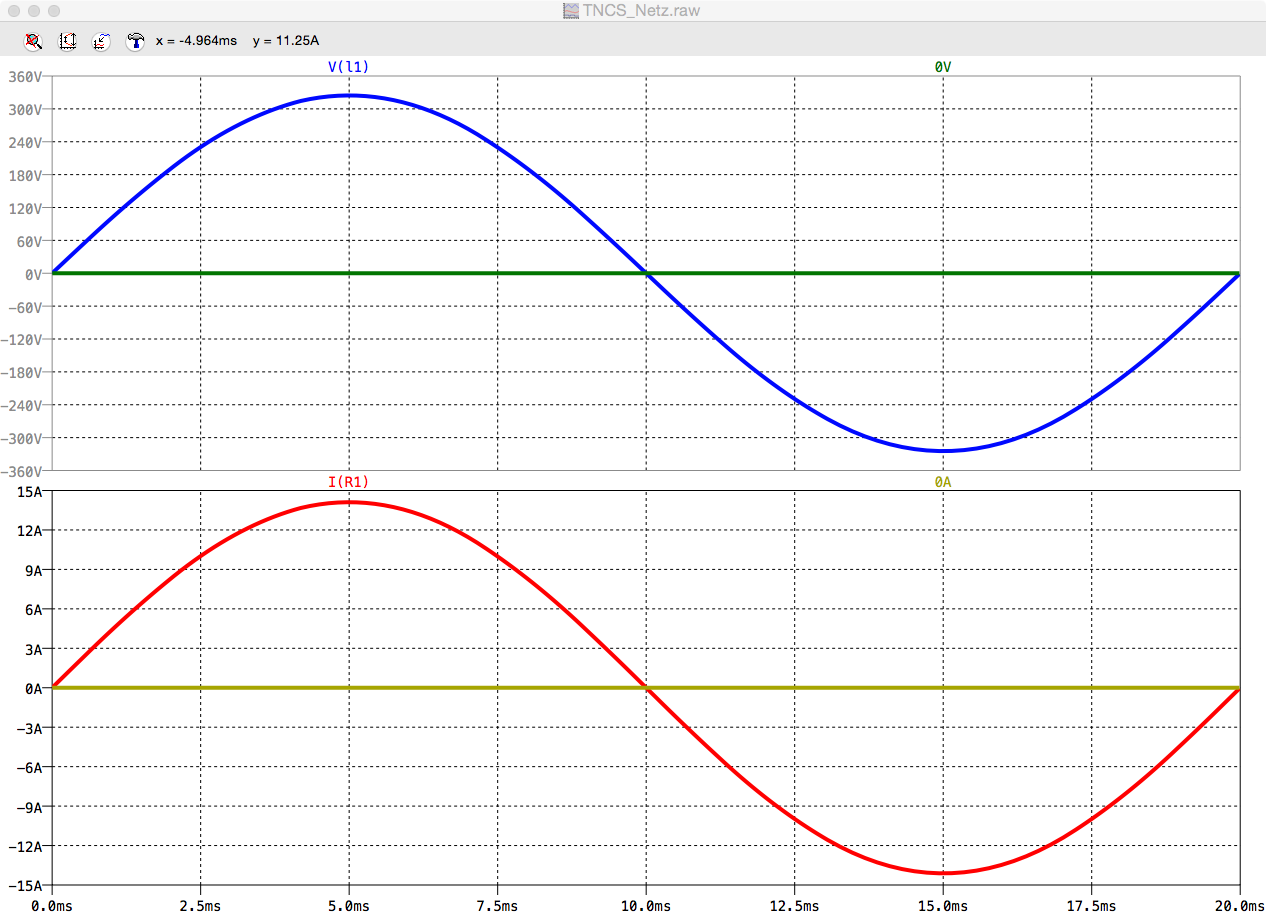
Kenngrößen des Wechselstroms

Der Wechselstrom hat einen sinusförmigen Verlauf. Während einer Periodendauer wechselt der Wechselstrom einmal seine Polarität.
Wichtige Kenngrößen des Wechselstromes sind Amplitude, Frequenz und Phasenverschiebung.

Liniendiagramm einer sinusförmigen Wechselspannung

Darstellungsfehler

Amplitude Umax in V
Frequenz f in Hz
Phasenverschiebung φ in Grad
Zeitintervall tmax in ms

Zeigerdiagramm

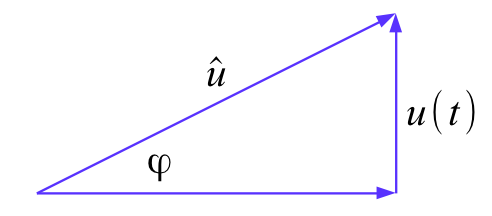
Eine sinusförmige Wechselgröße kann als rotierender Zeiger dargestellt werden. Der Zeiger rotiert mit der Winkelgeschwindigkeit

ω=φ/t   (1)

Das Verhältnis von Momentanwert u(t) (=Gegenkathete) zum Spitzenwert us (=Hypothenuse) ist die Definition der trigonometrischen Sinusfunktion:

sinφ=u(t)/us   (2)

Setzt man Gl. (1) in Gl. (2) ein, erhält man für den Momentanwert:

u(t)=us⋅sin(ω⋅t)

Berücksichtigt man, dass für eine Umdrehung mit der Periodendauer T gilt:

ω=2⋅π/T

und der Kehrwert der Periodendauer als Frequenz f definiert ist,erhält man:

u(t)=us⋅sin(2⋅π⋅f⋅t)

Simulation eines Wechselstromkreises

Begriff Erläuterung messtechnische Ermittlung
Amplitude us Die Maximalwert einer elektrischen Spannung oder Stromstärke. Oszilloskop
Periodendauer
T		 Ein vollständiger Schwingungsvorgang heißt Periode. Oszilloskop
Frequenz
f = 1/T		 Anzahl der Perioden pro Sekunde. Oszilloskop, Frequenzmesser
Effektivwert Spannungswert (oder Stromstärke) bei der Wechselstromspannungen (Wechselströme) die gleiche Leistung bewirkt wie bei Gleichspannung (Gleichstrom). Vielfachmessgerät


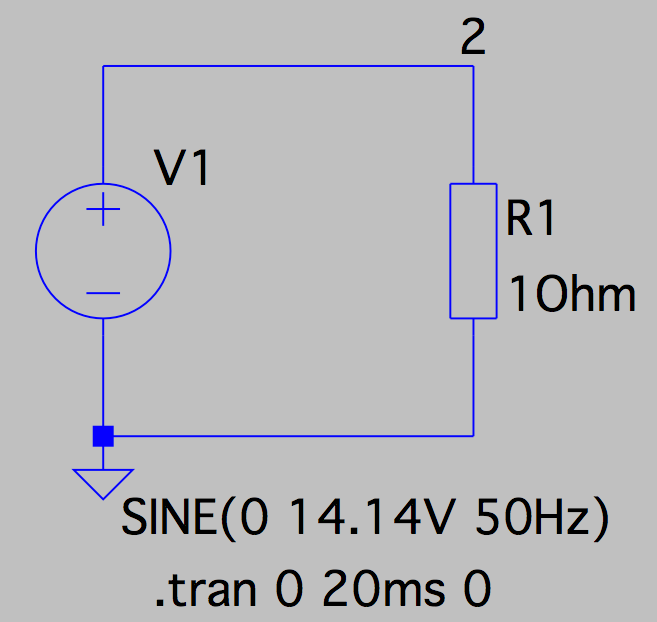
Spannungs, Strom und Leistungsverlauf


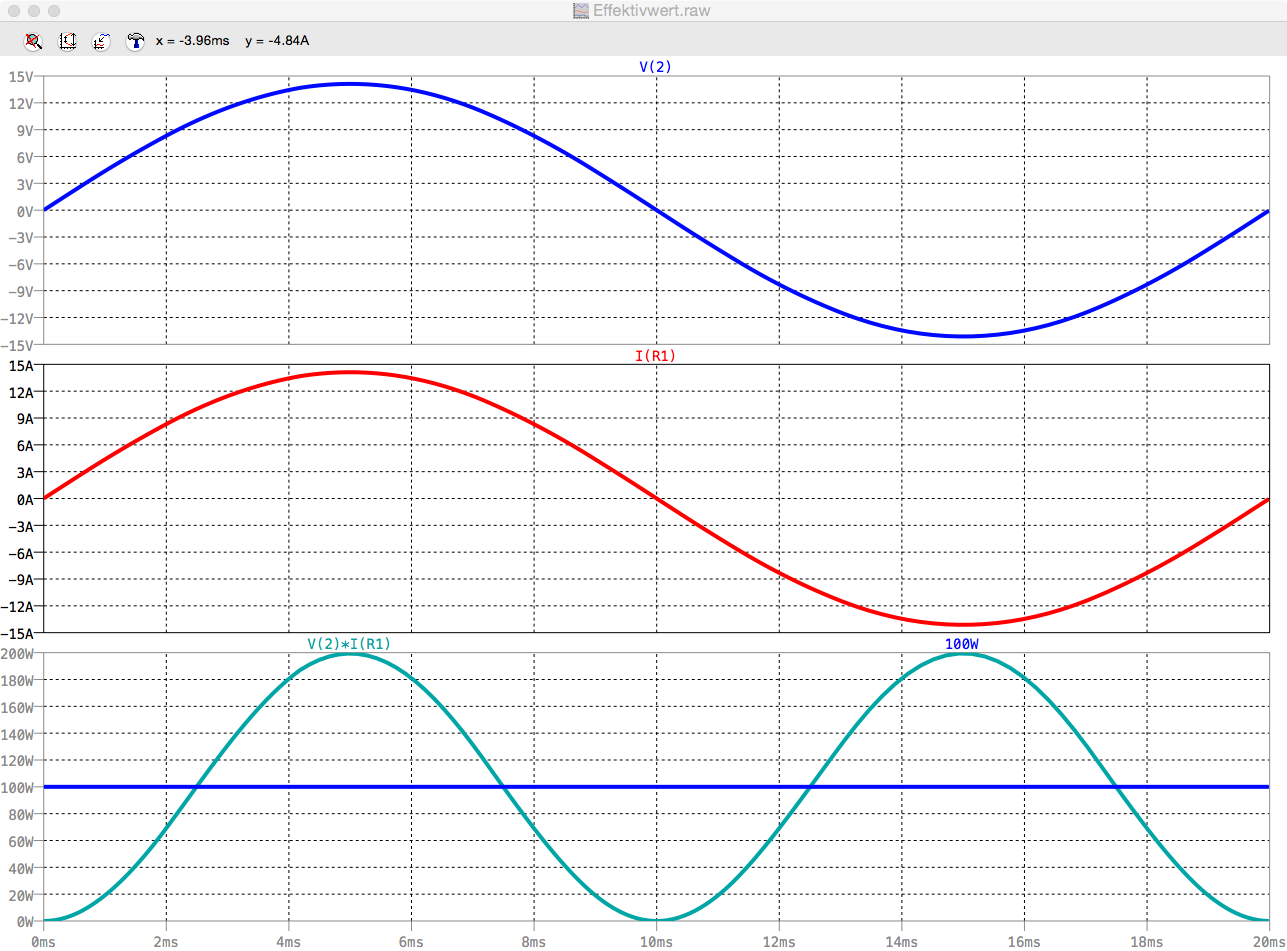
Der arithmetische Mittelwert der Leistung beträgt 100W.
Damit das Produkt aus Spannung und Strommstärke 100W ergibt, muss der Spitzenwert der Spannung (14,14V) und der Spitzenwert des Stromes (14,14A) jeweils durch die Wurzel von 2 (1,414) dividiert werden.
Um den Effektivwert einer Wechselspannung (Wechselstrom) zu ermitteln, muss der Spitzenwert durch die Wurzel von 2 dividiert werden.
Der Effektivwert einer Wechselspannung bewirkt in einem ohmschen Widerstand die gleiche Wärmeabgabe wie eine entsprechende Gleichspannung.
Beispiel aus der Praxis:
An einer Batterie wird mit einem Vielfachmessgerät in der Messschalterstellung AV eine Spannung von 10 V gemessen.
An der Sekundärwicklung eines Transformators (Wechselstromquelle) wird mit einem Vielfachmessgerät in der Messschalterstellung RMS eine Spannung von 10 V gemessen.
In beiden Fällen erzeugen die Spannungsquellen in einem Widerstand (z.B. 10 Ohm) die gleiche elektrische Leistung (10 W).

Aufgaben

  1. Wie ist die Sinusfunktion definiert?
  2. Was versteht man unter einer Amplitude?
  3. Was versteht man unter Phasenverschiebung?
  4. Was versteht man unter Momentanwert?
  5. Was versteht man unter Frequenz?
  6. Was versteht man unter Kreisfrequenz?
  7. Was versteht man unter Periodendauer?
  8. Zeichnen Sie ein Liniendiagramm für u(t) = 100V*sin(2 π 50 1/s t).
  9. Was versteht man unter Effektivwert? Wie wird der Effektivwert berechnet, wenn der Spitzenwert gegeben ist?
  10. Wie wird der Effektivwert einer Wechselspannung aus dem Liniendiagramm ermittelt?
  11. Der Spitzenwert einer Sinusförmigen Wechselspannung beträgt 325 V. Berechnen Sie den Effektivwert.
  12. Berechnen Sie den Momentanwert für t=5 ms (t=15 ms) einer 50 Hz-Wechselspannung. Der Spitzenwert beträgt 325 V.

Inhaltsverzeichnis