Der induktive Blindwiderstand
Unter induktiven Blindwiderstand versteht man den Widerstand einer
Spule im Wechselstromkreis.
Jede Leitung hat einen induktiven Blindwiderstand.
Die Ständerwicklungen von Asynchronmotoren haben einen induktiven
Blindwiderstand.
In Siebschaltungen (Frequenzweichen, Splitter) wird die
Frequenzabhängigkeit von induktiven Blindwiderständen genutzt.
Berechnung des induktiven Blindwiderstandes
Wenn man die Frequenz f erhöht, dann vergrößert sich der induktive Blindwiderstand. Der
induktive Blindwiderstand ist also proportional zur Frequenz. Je größer
die Frequenz, desto größer der induktive Blindwiderstand.
Gemessen wird der induktive Blindwiderstand mit einem
Vielfachmessgerät und einer Wechselspannungsquelle:
Spannung an der Spule messen. Stromstärke messen. Spannung durch
Stromstärke
teilen.
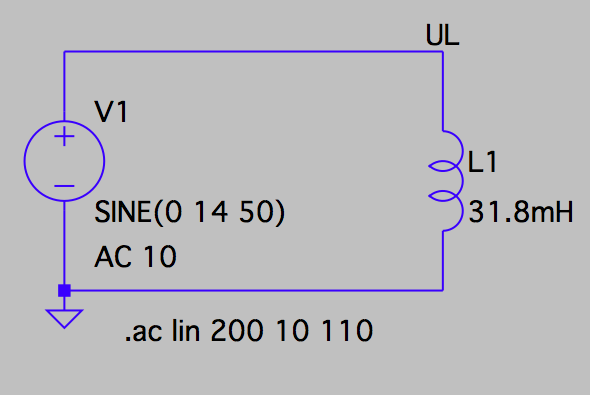
Messschaltung für den induktiven Blindwiderstand
Kennlinie XL = g(f)
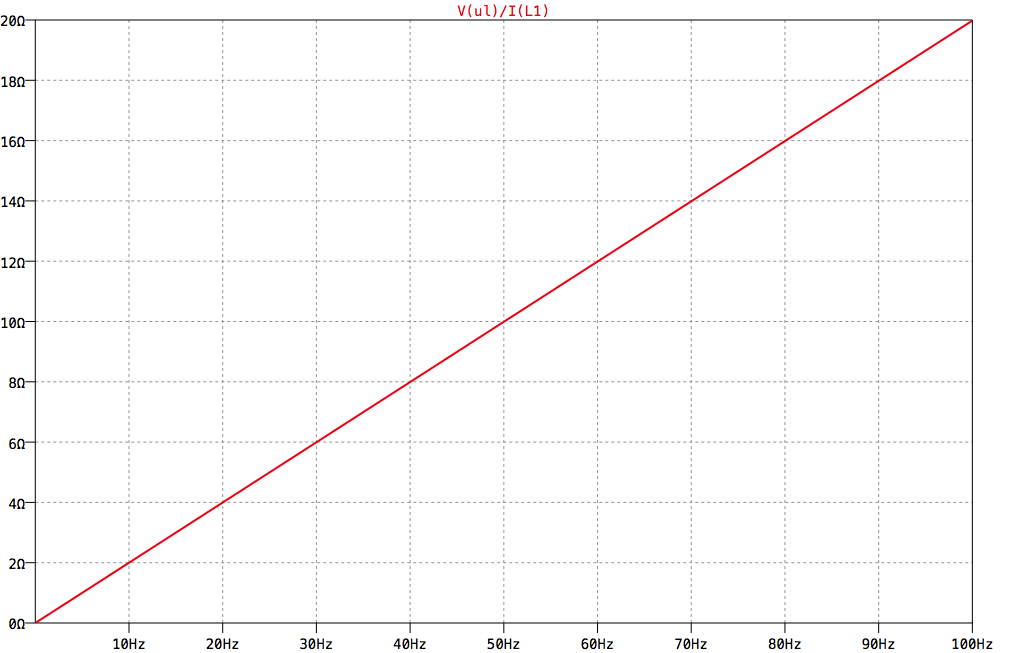
Aus der Kennlinie kann folgende Formel ermittelt werden:
XL = 2⋅π⋅f⋅L
Messschaltung für die Blindleistung
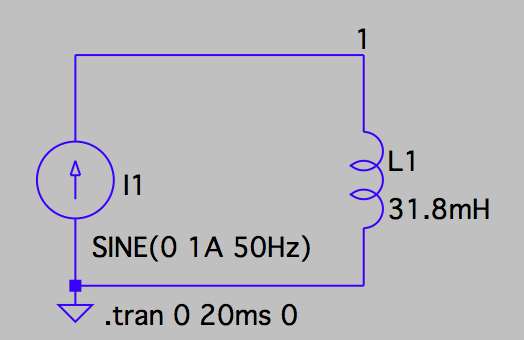
Ein konstanter Strom von 1A fließt durch die Spule. Der induktive Spannungsfall wird mit dem Strom multipliziert.
Liniendiagramm der Blindleistung
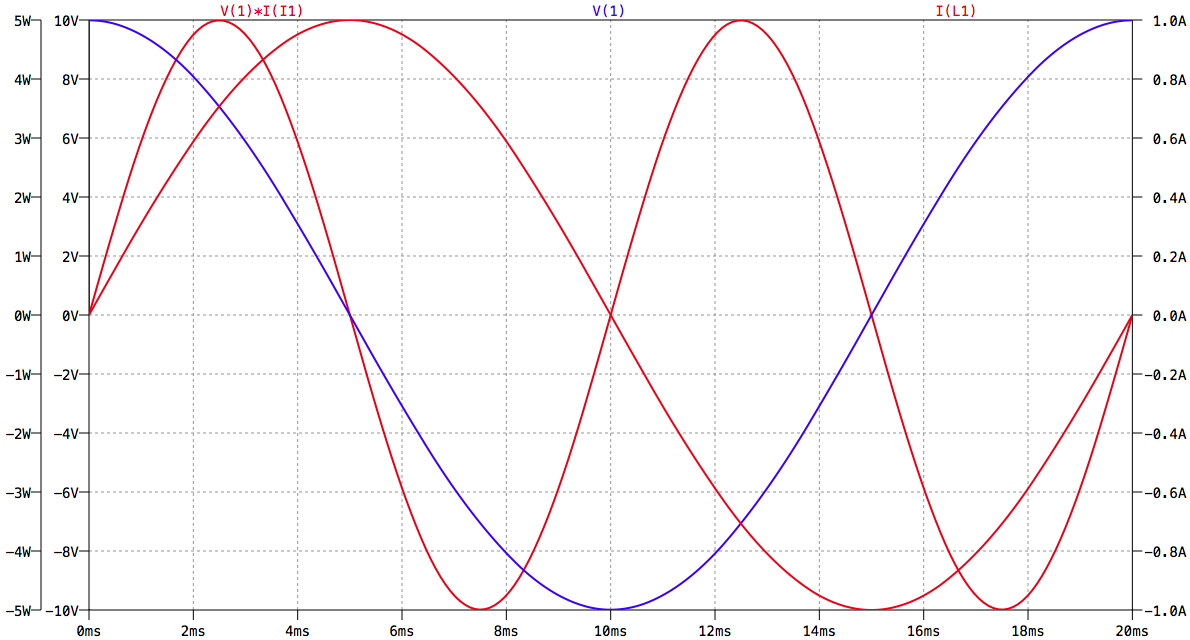
Die Phasenverschiebung zwischen Strom und Spannung beträgt 90°. Der Strom eilt der Spannung um 90° nach.
Das arithmetische Mittel der Fläche unter der Leistungskurve (= el.
Arbeit) ist null. Deshalb findet kein Leistungsumsatz statt. Das
Produkt aus Spulenspannung und Spulenstrom nennt man Blindleistung. Die
Blindleistung einer Spule wird wie folgt berechnet:
QL= UL⋅I oder QL= XL⋅IL2
oder QL= UL2/XL
Aufgaben
- Eine Spule mit einer Induktivität von L=31,8 mH ist an eine
Stromquelle I=1 A angeschlossen. Die Stromquelle liefert eine
sinusförmigen Stromverlauf mit einer Frequenz von f=50 Hz. Simulieren
Sie den Spannungs- und Stromverlauf. Welche Phasenverschiebung besteht
zwischen Spannung und Stromstärke. Wie groß ist der induktive
Blindwiderstand? Verdoppeln Sie die Induktivität und ermitteln Sie den
induktiven Blindwiderstand. Verdoppeln Sie die Frequenz und ermitteln
Sie den induktiven Blindwiderstand. Interpretieren Sie die Ergebnisse.
Simulieren Sie die induktive Blindleistung Q=U⋅I.
- Was versteht man unter induktiver Blindleistung?
- Eine Spule mit einer Induktivität von 12 mH (6 mH) wird an eine
Spannungsquelle mit der Frequenz von 50 Hz (100 Hz) angeschlossen.
Berechnen Sie den induktiven Blindwiderstand.
- Eine Spule wird an eine Spannungsquelle (U= 24 V) mit der
Frequenz von 50 Hz angeschlossen. Es fließt ein Strom von 2 A.
Berechnen Sie die Induktivität.
- Eine Spule mit einer Induktivität von 24 mH wird an eine
Spannungsquelle mit 12 V angeschlossen. Es fließt ein Strom von 0,5 A.
Berechnen Sie die Frequenz.
- Welchen Wert muss eine Induktivtät haben, wenn der induktive
Blindwiderstand 120 Ω im 50 Hz-Netz betragen soll?
- Welcher Zusammenhang besteht zwischen Frequenz und induktiven
Blindwiderstand?
- Welcher Zusammenhang besteht zwischen Induktivität und induktiven
Blindwiderstand?
- Durch einen induktiven Blindwiderstand von 12 Ω fließt ein Strom
von 2 A. Berechnen Sie die Blindleistung.
- Ein induktiver Blindwiderstand von 115 Ω ist an eine Spannung von
230 V angeschlossen. Berechnen Sie die Blindleistung.
Reihenschaltung von Spule und Widerstand
In der Praxis kommt eine Reihenschaltung aus einer Spule und einem
Widerstand in Leuchtstoffröhrenschaltungen vor. Die Leuchstoffröhre hat
einen ohmschen Widerstand die Vorschaltdrossel (=Spule) ist dazu in
Reihe geschaltet.
Messschaltung
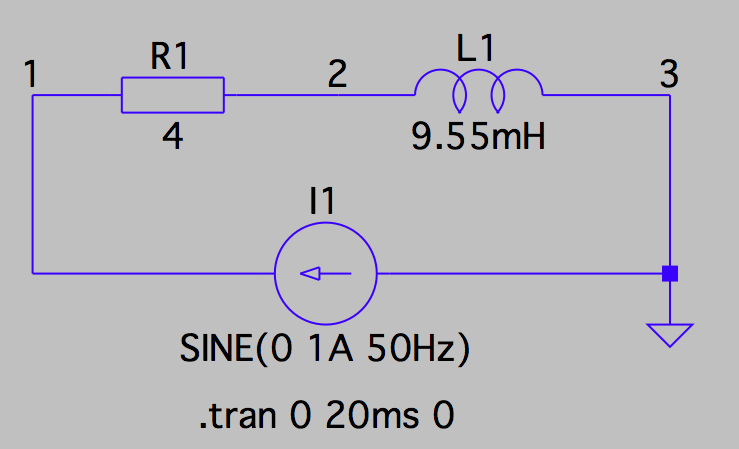
Wenn ein Strom von 1 A durch den ohmschen Widerstand R1
fließt, dann muss an diesem Widerstand eine Spannung von 4 V abfallen.
Liniendiagramm der Spannungen
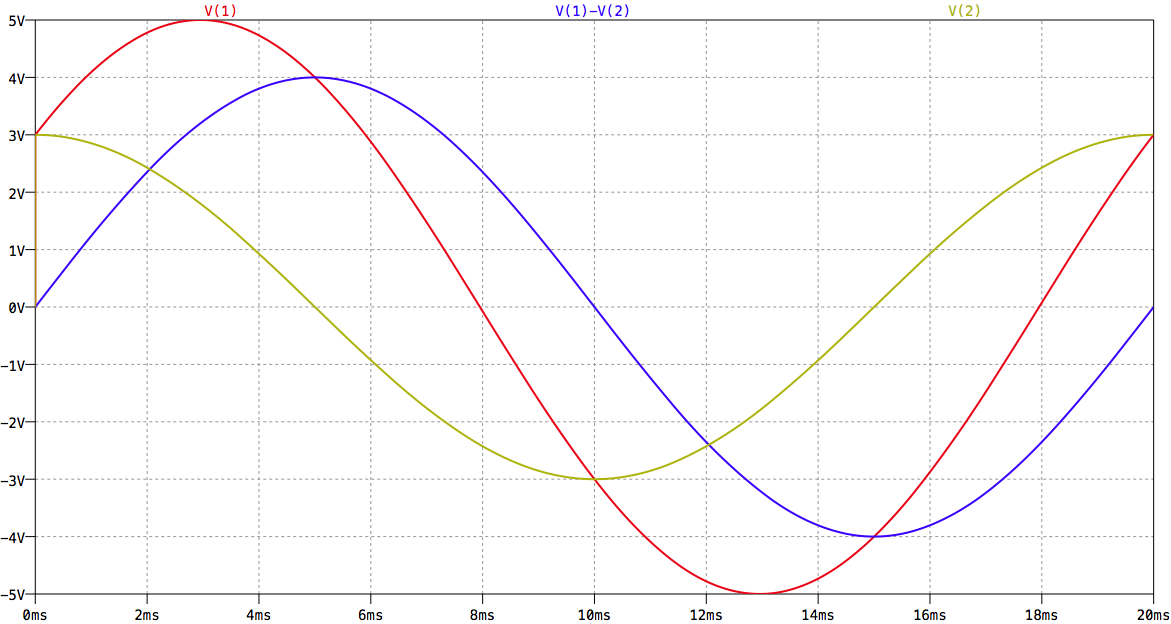
Die Phasenverschiebung zwischen der Spannung am Widerstand und der
Spannung an der Spule beträgt 90°.
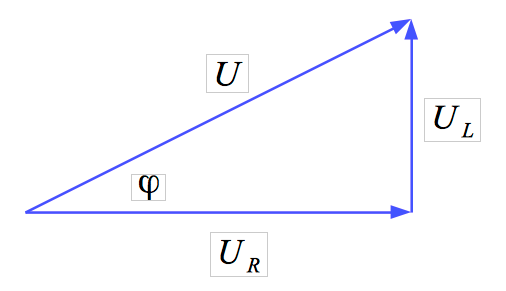
Spannungsdreieck
Das Zeigerdiagramm für die Spannungen lässt sich aus dem Liniendiagramm
entwickeln.
| Zeigerdiagramm |
Formeln |
|
Gesamtspannung
|
U2 = UR2 + UL2
|
| Spannungsfall am Widerstand |
UR = U⋅cos φ |
| Spannungsfall an der Spule |
UL = U⋅sin φ
|
| Leistungsfaktor |
cos φ = UR/U |
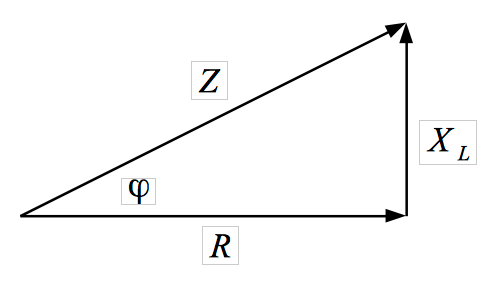
Widerstandsdreieck
Das Zeigerdiagramm für die Widerstände lässt sich aus dem
Spannungsdreieck entwickeln. Jede Spannung aus dem Spannungsdeieck
wird durch die Stromstärke dividiert.
| Zeigerdiagramm |
Formeln |
|
Scheinwiderstand
|
Z2 = R2 + XL2
|
Wirkwiderstand
|
R = Z⋅cos φ
|
Blindwiderstand
|
XL = Z⋅sin φ
|
| Leistungsfaktor
|
cos φ = R/Z
|
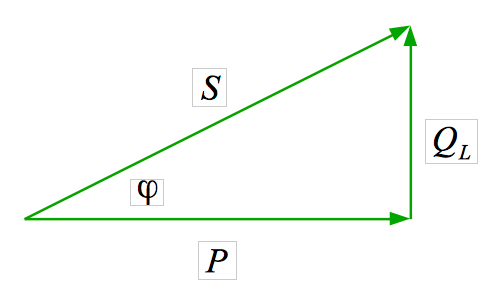
Leistungsdreieck
Das Zeigerdiagramm für die Leistungen lässt sich aus dem
Spannungsdreieck entwickeln. Jede Spannung aus dem Spannungsdeieck wird
mit der Stromstärke multipliziert.
| Zeigerdiagramm |
Formeln |
|
Scheinleistung
|
S = U⋅I
S2 = P2 + QL2 |
| Wirkleistung |
P = S⋅cos φ
|
| Blindleistung |
QL = S⋅sin φ |
| Leistungsfaktor |
cos φ = P/S |
Der Leistungsfaktor hat einen Wert zwischen 0 und 1. Wenn der
Leistungsfaktor klein ist, dann ist der Anteil der induktiven
Blindleistung groß. Wenn der Leistungsfaktor groß ist, dann ist der
Anteil der induktiven Blindleistung klein.
Simulation der Blindleistung
Der Phasenverschiebungswinkel zwischen Spannung (blau) und Stromstärke (rot)
bestimmt den Anteil der Blindleistung (grün).
Wenn der Phasenverschiebungswinkel 90° beträgt, ist der arithmetische
Mittelwert der Fläche unter der Leistungskurve (el. Arbeit) einer
Periode null. Eine Spule nimmt also im Wechselstromkreis keine
Wirkleistung auf. Weil nach jedem Nulldurchgang mit negativer Steigung
die aufgenommene Energie
wieder an die Spannungsquelle zurückgegeben wird, findet
in der Spule kein Leistungsumsatz statt. Deshalb spricht man von
Blindleistung.
Vollständige Berechnung der Reihenschaltung
Nachfolgend können der Gesamtwiderstand Z, die Spannungsfälle und
Leistungen der Reihenschaltung berechnet werden.
Aufgaben
- Zeichnen Sie das Zeigerdiagramm der Spannungen.
- Entwickeln Sie aus dem Zeigerdiagramm der Spannungen das Zeigerdiagramm der Widerstände.
- Entwickeln Sie aus dem Zeigerdiagramm der Spannungen das Zeigerdiagramm der Leistungen.
- Was versteht man unter Scheinleistung? Wie wird die Scheinleistung gemessen und berechnet?
- Gegeben sind der Spannungsfall am Widerstand und an der Spule.
Stellen Sie eine Formel für die Berechnung der Gesamtspannung auf.
- Gegeben sind der ohmsche Widerstand R und induktive
Blindwiderstand XL. Stellen Sie eine Formel für die Berechnung der
Impedanz Z auf.
- Gegeben sind die Wirkleistung P und die Blindleistung Q. Stellen Sie eine Formel für die Berechnung der Scheinleistung S auf.
- Welche Beziehung besteht zwischen Scheinleistung und Wirkleistung?
- Die Blindleistung einer Reihenschaltung aus R und L soll gemessen
werden. Zeichnen Sie die Messschaltung und beschreiben Sie das
Messverfahren.
- Von einer Reihenschaltung sind folgende Werte gegeben R = 6 Ω und XL = 8 Ω.
Berechnen Sie die Impedanz.
- Von einer Reihenschaltung sind folgende Werte gegeben P = 16 W und QL = 12 var. Berechnen Sie die Scheinleistung.
- Die Impedanz beträgt 5 Ω. Der ohmsche Widerstand hat einen Wert von 3 Ω.
Berechnen Sie den induktiven Blindwiderstand.
- Von einer Reihenschaltung sind folgende Werte gegeben P =
12 W und S = 13 VA. Berechnen Sie die Blindleistung und den
Leistungsfaktor.
- Eine Reihenschaltung aus R= 10 Ω und XL = 20 Ω ist an 230 V (50
Hz) angeschlossen. Zeichnen Sie das Zeigerdiagramm der Widerstände.
Berechnen Sie die Impedanz, die Stromstärke, die Spannungsfälle, die
Wirkleistung, die Blindleistung, die Scheinleistung und den
Leistungsfaktor.
- Eine Reihenschaltung aus R und L ist an 230 V (50 Hz)
angeschlossen. Der Leistungsfaktor beträgt 0,95. Es fließt ein Strom
von 3,2 A. Berechnen Sie R und L.









